
 |

gunkiemike
Sep 2, 2010, 9:12 PM
Post #51 of 100
(7875 views)
Shortcut
Registered: Oct 1, 2002
Posts: 2266
|
curt wrote: I have little doubt we'll see the "correct" answer posted here in short order: http://www.theclimbinglab.com ...as soon as the proctor, the advisory board and the dumbass get around to it.  Curt
Jesus, give it up already...
|
|
|
 |
 |

gunkiemike
Sep 2, 2010, 9:18 PM
Post #52 of 100
(7875 views)
Shortcut
Registered: Oct 1, 2002
Posts: 2266
|
ptlong2 wrote: I think it's simpler if this obvious complication is ignored. Pretend there are no ledges below and no obstacles in the way, other than that vertical wall or big corner that the climber could pendulum into. Is adding slack (how much?) going to reduce the speed that the climber impacts the wall/corner?
If we think like physics students and resolve the fall into horizontal and vertical components, I suspect we see that the horizontal component of the climber's ultimate (bottom of fall) motion is unaffected by slack. So he impacts the wall with V(sub)h. Adding slack merely increases his V(sub)v, the vertical component of the fall. In other words, with slack he strikes the wall at a glancing blow; without slack he hits it perpendicularly. I think I'd want the former. Within reasonable limits.
|
|
|
 |
 |

Rudmin
Sep 2, 2010, 9:20 PM
Post #53 of 100
(7874 views)
Shortcut
Registered: Mar 29, 2009
Posts: 606
|
how would you get a vertical component of velocity at the bottom of a fall? If you are still moving vertically you are still falling.
|
|
|
 |
 |

gunkiemike
Sep 2, 2010, 9:31 PM
Post #54 of 100
(7868 views)
Shortcut
Registered: Oct 1, 2002
Posts: 2266
|
Rudmin wrote: how would you get a vertical component of velocity at the bottom of a fall? If you are still moving vertically you are still falling.
Good point - I'm picturing the rope tension being sufficient to produce the horizontal motion of the climber BEFORE the tension rises high enough and long enough to arrest the vertical component. That may not be the case.
[goes back to scratching his head]
|
|
|
 |
 |

blondgecko
Moderator
Sep 2, 2010, 11:46 PM
Post #55 of 100
(7839 views)
Shortcut
Registered: Jul 2, 2004
Posts: 7666
|
blondgecko wrote: ptlong2 wrote: Like this?  About how much slack would you add? One somewhat unintuitive thing the climber could do in this situation is, if possible, launch himself back towards the belayer as he comes off. The closer to directly underneath the last anchor point he is when tension comes onto the rope, the better off he's going to be.
So, I decided to some quick back-of-the-envelope calculations on this idea (sorry, don't have time to do a real analysis).
To simplify, say you're on a perfectly inelastic rope with no slack 3m horizontally from a pivot point. You drop and start to pendulum until you're 1m vertically below your starting point. At this point your anchor instantly extends by 1m.
Under this scenario, according to my calculations at the instant the anchor extends, you're travelling at ~4.2m/s vertically, 1.5m/s horizontally, and you're 1m vertically and 2m horizontally from your anchor. Once the anchor extends, however, you're in free-fall and not being accelerated by the rope until it pulls tight again (ie. when the distance from the original pivot point = 4m).
Until that happens, it's just plain old parabolic trajectory: V(horizontal) = 1.5m/s; V(vertical) = 4.2m/s + 9.81*t.
If I haven't made a mistake along the way, this means that you re-engage the rope after a little over 0.4 seconds, by which time you're ~2.75m lower, and 0.65m closer to the wall. At that instant, you're moving at ~8.5m/s vertically, but still moving at just 1.5m/s horizontally. By comparison, at this time in the straight pendulum, your fall would be almost over and you'd be about to hit the wall at a little over 7m/s. So not only are you going far slower in the direction that's going to hurt, but your angle with the anchor point at the instant of re-engagement is now only about 20 degrees from vertical (it was 65 degrees when the anchor shifted) - meaning that a far greater fraction of the fall energy will go into stretching the rope rather than accelerating you sideways.
It's been a long, long time since I had anything to do with spring calculations, so I'll leave it to someone else, if interested, to do the detailed calculations.
|
|
|
 |
 |

blondgecko
Moderator
Sep 3, 2010, 1:10 AM
Post #56 of 100
(7820 views)
Shortcut
Registered: Jul 2, 2004
Posts: 7666
|
blondgecko wrote: blondgecko wrote: ptlong2 wrote: Like this?  About how much slack would you add? One somewhat unintuitive thing the climber could do in this situation is, if possible, launch himself back towards the belayer as he comes off. The closer to directly underneath the last anchor point he is when tension comes onto the rope, the better off he's going to be. So, I decided to some quick back-of-the-envelope calculations on this idea (sorry, don't have time to do a real analysis). To simplify, say you're on a perfectly inelastic rope with no slack 3m horizontally from a pivot point. You drop and start to pendulum until you're 1m vertically below your starting point. At this point your anchor instantly extends by 1m. Under this scenario, according to my calculations at the instant the anchor extends, you're travelling at ~4.2m/s vertically, 1.5m/s horizontally, and you're 1m vertically and 22.8m horizontally from your anchor. Once the anchor extends, however, you're in free-fall and not being accelerated by the rope until it pulls tight again (ie. when the distance from the original pivot point = 4m). Until that happens, it's just plain old parabolic trajectory: V(horizontal) = 1.5m/s; V(vertical) = 4.2m/s + 9.81*t. If I haven't made a mistake along the way, this means that you re-engage the rope after a little overunder 0.4 seconds, by which time you're ~ 2.752.3m lower, and 0.650.56m closer to the wall. At that instant, you're moving at ~ 8.57.9m/s vertically, but still moving at just 1.5m/s horizontally. By comparison, at this time in the straight pendulum, your fall would be almost over and you'd be about to hit the wall at a little over 7m/s. So not only are you going far slower in the direction that's going to hurt, but your angle with the anchor point at the instant of re-engagement is now only about 2035 degrees from vertical (it was 6570 degrees when the anchor shifted) - meaning that a far greater fraction of the fall energy will go into stretching the rope rather than accelerating you sideways. It's been a long, long time since I had anything to do with spring calculations, so I'll leave it to someone else, if interested, to do the detailed calculations.
Murphy's law strikes (it's sin, not cos). I think that's right now.
|
|
|
 |
 |

curt
Sep 3, 2010, 1:11 AM
Post #57 of 100
(7820 views)
Shortcut
Registered: Aug 27, 2002
Posts: 18275
|
gunkiemike wrote: curt wrote: I have little doubt we'll see the "correct" answer posted here in short order: http://www.theclimbinglab.com ...as soon as the proctor, the advisory board and the dumbass get around to it.  Curt Jesus, give it up already...
Hey, thanks for the unsolicited and unwanted advice.
Curt
|
|
|
 |
 |

blondgecko
Moderator
Sep 3, 2010, 2:02 AM
Post #58 of 100
(7804 views)
Shortcut
Registered: Jul 2, 2004
Posts: 7666
|
blondgecko wrote: blondgecko wrote: blondgecko wrote: ptlong2 wrote: Like this? [img]http://img825.imageshack.us/img825/3360/horizontala.jpg[/img] About how much slack would you add? One somewhat unintuitive thing the climber could do in this situation is, if possible, launch himself back towards the belayer as he comes off. The closer to directly underneath the last anchor point he is when tension comes onto the rope, the better off he's going to be. So, I decided to some quick back-of-the-envelope calculations on this idea (sorry, don't have time to do a real analysis). To simplify, say you're on a perfectly inelastic rope with no slack 3m horizontally from a pivot point. You drop and start to pendulum until you're 1m vertically below your starting point. At this point your anchor instantly extends by 1m. Under this scenario, according to my calculations at the instant the anchor extends, you're travelling at ~4.2m/s vertically, 1.5m/s horizontally, and you're 1m vertically and 22.8m horizontally from your anchor. Once the anchor extends, however, you're in free-fall and not being accelerated by the rope until it pulls tight again (ie. when the distance from the original pivot point = 4m). Until that happens, it's just plain old parabolic trajectory: V(horizontal) = 1.5m/s; V(vertical) = 4.2m/s + 9.81*t. If I haven't made a mistake along the way, this means that you re-engage the rope after a little overunder 0.4 seconds, by which time you're ~ 2.752.3m lower, and 0.650.56m closer to the wall. At that instant, you're moving at ~ 8.57.9m/s vertically, but still moving at just 1.5m/s horizontally. By comparison, at this time in the straight pendulum, your fall would be almost over and you'd be about to hit the wall at a little over 7m/s. So not only are you going far slower in the direction that's going to hurt, but your angle with the anchor point at the instant of re-engagement is now only about 2035 degrees from vertical (it was 6570 degrees when the anchor shifted) - meaning that a far greater fraction of the fall energy will go into stretching the rope rather than accelerating you sideways. It's been a long, long time since I had anything to do with spring calculations, so I'll leave it to someone else, if interested, to do the detailed calculations. Murphy's law strikes (it's sin, not cos). I think that's right now.
OK, colour me obsessed, but I worked out the "perfect" case (where the climber hits the wall just as the rope comes taught again, which unless I'm missing something will give the lowest possible horizontal speed) for two scenarios: a 1m or 2m extension at the anchor. Here it is graphically (trajectories are a bit rough, but distances and velocity vectors (the blue arrows) are to scale):

Basically, if you do nothing your horizontal velocity at impact is 7.7m/s. If you instantaneously release 1m of slack when the climber's at the point of the trajectory marked by the rightmost orange circle, he'll be going at 5.8m/s horizontally when he hits the wall (at the point marked by the bottom orange circle). If you release 2m of slack at the point of the rightmost purple circle, he'll be going just 4.5m/s at the wall. Since kinetic energy scales as the square, that's a 42 and 66% reduction in horizontal impact energy, respectively.
|
|
Attachments:
|
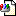 pendulum.gif
(6.65 KB)
pendulum.gif
(6.65 KB)
|
|
|
 |
 |

112
Sep 3, 2010, 2:40 AM
Post #59 of 100
(7797 views)
Shortcut
Registered: May 15, 2004
Posts: 432
|
I think you are modeling a dynamic belay with no slack to start. I thought the question was regarding how much initial slack to add, and then the motion would be mostly rotational there after. I see it as: fall, initial catch, and then penji.
45 degrees seems optimal (as jt512 stated); slack to pay out would be roughly 40% of the distance from last pro. But, if someone worked out an equation to optimize, that would be cool!
|
|
|
 |
 |

blondgecko
Moderator
Sep 3, 2010, 3:37 AM
Post #60 of 100
(7775 views)
Shortcut
Registered: Jul 2, 2004
Posts: 7666
|
112 wrote: I think you are modeling a dynamic belay with no slack to start. I thought the question was regarding how much initial slack to add, and then the motion would be mostly rotational there after. I see it as: fall, initial catch, and then penji. 45 degrees seems optimal (as jt512 stated); slack to pay out would be roughly 40% of the distance from last pro. But, if someone worked out an equation to optimize, that would be cool!
Yes, I'm modelling an alternative scenario. The basic idea I'm putting forward is that the best time to provide slack isn't before the fall. It's during the fall, once the climber has built up some sideways momentum.
|
|
|
 |
 |

jt512
Sep 3, 2010, 3:45 AM
Post #61 of 100
(7771 views)
Shortcut
Registered: Apr 12, 2001
Posts: 21904
|
blondgecko wrote: 112 wrote: I think you are modeling a dynamic belay with no slack to start. I thought the question was regarding how much initial slack to add, and then the motion would be mostly rotational there after. I see it as: fall, initial catch, and then penji. 45 degrees seems optimal (as jt512 stated); slack to pay out would be roughly 40% of the distance from last pro. But, if someone worked out an equation to optimize, that would be cool! Yes, I'm modelling an alternative scenario. The basic idea I'm putting forward is that the best time to provide slack isn't before the fall. It's during the fall, once the climber has built up some sideways momentum.
That seems counterintuitive.
Jay
|
|
|
 |
 |

blondgecko
Moderator
Sep 3, 2010, 3:54 AM
Post #62 of 100
(7763 views)
Shortcut
Registered: Jul 2, 2004
Posts: 7666
|
jt512 wrote: blondgecko wrote: 112 wrote: I think you are modeling a dynamic belay with no slack to start. I thought the question was regarding how much initial slack to add, and then the motion would be mostly rotational there after. I see it as: fall, initial catch, and then penji. 45 degrees seems optimal (as jt512 stated); slack to pay out would be roughly 40% of the distance from last pro. But, if someone worked out an equation to optimize, that would be cool! Yes, I'm modelling an alternative scenario. The basic idea I'm putting forward is that the best time to provide slack isn't before the fall. It's during the fall, once the climber has built up some sideways momentum. That seems counterintuitive. Jay
Yes it does - so don't take my word for it, but do the working yourself. The basic idea is simple, though - as long as the falling climber is moving sideways without being supported by the rope, they're reducing the horizontal fraction of the force imparted by the rope once it comes tight.
|
|
|
 |
 |

jt512
Sep 3, 2010, 4:06 AM
Post #63 of 100
(7757 views)
Shortcut
Registered: Apr 12, 2001
Posts: 21904
|
blondgecko wrote: jt512 wrote: blondgecko wrote: 112 wrote: I think you are modeling a dynamic belay with no slack to start. I thought the question was regarding how much initial slack to add, and then the motion would be mostly rotational there after. I see it as: fall, initial catch, and then penji. 45 degrees seems optimal (as jt512 stated); slack to pay out would be roughly 40% of the distance from last pro. But, if someone worked out an equation to optimize, that would be cool! Yes, I'm modelling an alternative scenario. The basic idea I'm putting forward is that the best time to provide slack isn't before the fall. It's during the fall, once the climber has built up some sideways momentum. That seems counterintuitive. Jay Yes it does - so don't take my word for it, but do the working yourself. The basic idea is simple, though - as long as the falling climber is moving sideways without being supported by the rope, they're reducing the horizontal fraction of the force imparted by the rope once it comes tight.
Actually, now that I think about it, not only is it intuitive, but I have always performed a variant of it. As I said in an earlier post, when the leader is to the side of his pro, in addition to leaving slack in the rope, I also give a dynamic belay. The latter accomplishes something similar to what you are suggesting: lengthening the fall at the last instant before impact with the wall. Intuitively, I always suspected that the dynamic belay part was more important than the initial slack. But whatever method one choses to lengthen the fall at the last moment, one can still leave initial slack in the rope, and so the question of the effectiveness of that remains open.
Jay
(This post was edited by jt512 on Sep 3, 2010, 4:07 AM)
|
|
|
 |
 |

hafilax
Sep 3, 2010, 5:14 AM
Post #64 of 100
(7741 views)
Shortcut
Registered: Dec 12, 2007
Posts: 3025
|
I think that for this kind of problem one can learn more with a fishing bob and an elastic or a piece of string than from crunching numbers.
|
|
|
 |
 |

Rudmin
Sep 3, 2010, 2:55 PM
Post #65 of 100
(7706 views)
Shortcut
Registered: Mar 29, 2009
Posts: 606
|
112 wrote: I think you are modeling a dynamic belay with no slack to start. I thought the question was regarding how much initial slack to add, and then the motion would be mostly rotational there after. I see it as: fall, initial catch, and then penji. 45 degrees seems optimal (as jt512 stated); slack to pay out would be roughly 40% of the distance from last pro. But, if someone worked out an equation to optimize, that would be cool!
I answered this question about a page ago. Slack doesn't help unless you add a lot of it, at least with a theoretical rope in a theoretical situation.
|
|
|
 |
 |

112
Sep 3, 2010, 3:12 PM
Post #66 of 100
(7696 views)
Shortcut
Registered: May 15, 2004
Posts: 432
|
Rudmin wrote: 112 wrote: I think you are modeling a dynamic belay with no slack to start. I thought the question was regarding how much initial slack to add, and then the motion would be mostly rotational there after. I see it as: fall, initial catch, and then penji. 45 degrees seems optimal (as jt512 stated); slack to pay out would be roughly 40% of the distance from last pro. But, if someone worked out an equation to optimize, that would be cool! I answered this question about a page ago. Slack doesn't help unless you add a lot of it, at least with a theoretical rope in a theoretical situation.
Yeah, you stated that, I guess I just didn't follow your proof. I am not doubting you. I just don't yet see the truth.
|
|
|
 |
 |

Rudmin
Sep 3, 2010, 3:20 PM
Post #67 of 100
(7691 views)
Shortcut
Registered: Mar 29, 2009
Posts: 606
|
112 wrote: Rudmin wrote: 112 wrote: I think you are modeling a dynamic belay with no slack to start. I thought the question was regarding how much initial slack to add, and then the motion would be mostly rotational there after. I see it as: fall, initial catch, and then penji. 45 degrees seems optimal (as jt512 stated); slack to pay out would be roughly 40% of the distance from last pro. But, if someone worked out an equation to optimize, that would be cool! I answered this question about a page ago. Slack doesn't help unless you add a lot of it, at least with a theoretical rope in a theoretical situation. Yeah, you stated that, I guess I just didn't follow your proof. I am not doubting you. I just don't yet see the truth.
My proof was a an excel sheet of forces, velocities, and positions calculated with a 1 ms time step. I can email it to you if you want..
|
|
|
 |
 |

blondgecko
Moderator
Sep 3, 2010, 8:06 PM
Post #68 of 100
(7662 views)
Shortcut
Registered: Jul 2, 2004
Posts: 7666
|
Rudmin wrote: 112 wrote: Rudmin wrote: 112 wrote: I think you are modeling a dynamic belay with no slack to start. I thought the question was regarding how much initial slack to add, and then the motion would be mostly rotational there after. I see it as: fall, initial catch, and then penji. 45 degrees seems optimal (as jt512 stated); slack to pay out would be roughly 40% of the distance from last pro. But, if someone worked out an equation to optimize, that would be cool! I answered this question about a page ago. Slack doesn't help unless you add a lot of it, at least with a theoretical rope in a theoretical situation. Yeah, you stated that, I guess I just didn't follow your proof. I am not doubting you. I just don't yet see the truth. My proof was a an excel sheet of forces, velocities, and positions calculated with a 1 ms time step. I can email it to you if you want..
If you're feeling enthusiastic, I'd love to see what your model says about my scenario(s) above.
|
|
|
 |
 |

Rudmin
Sep 3, 2010, 9:00 PM
Post #69 of 100
(7651 views)
Shortcut
Registered: Mar 29, 2009
Posts: 606
|
You can mess around with it all you like. To simulate what you said, I just took a 0 slack fall, and then took the position and velocity part way through and used those as initial conditions for a 3 metre slack fall. Not a very big difference.
Here is the excel sheet:
http://FastFreeFileHosting.com/...45/pendulum-xls.html
|
|
|
 |
 |

blondgecko
Moderator
Sep 3, 2010, 9:20 PM
Post #70 of 100
(7646 views)
Shortcut
Registered: Jul 2, 2004
Posts: 7666
|
Rudmin wrote: You can mess around with it all you like. To simulate what you said, I just took a 0 slack fall, and then took the position and velocity part way through and used those as initial conditions for a 3 metre slack fall. Not a very big difference. Here is the excel sheet: http://FastFreeFileHosting.com/...45/pendulum-xls.html
It won't let me download it - I get a message about the server not allowing proxies to download.
|
|
|
 |
 |

112
Sep 4, 2010, 12:24 AM
Post #71 of 100
(7622 views)
Shortcut
Registered: May 15, 2004
Posts: 432
|
I have been trying to put something together, but want to proof it before posting. But, it appears that adding up to 10% initial slack (of distance from last pro) increases the horizontal velocity at impact. Adding 20% slack is roughly the same as no slack and anything greater than 20% reduces the total horizontal velocity at impact.
I might be wrong (typically am), and this doesn't address which single form of mitigation (initial slack or dynamic belay) is better. I guess that analysis would be per foot of extension; which method is is more effective?
I am off for a 5-day weekend! I might post something when I return...
Thanks so much for such a fun thread!
EDit to add: Rudmin's number show the same thing but a cross over around 30%.
(This post was edited by 112 on Sep 4, 2010, 1:29 AM)
|
|
|
 |
 |

112
Sep 4, 2010, 1:49 AM
Post #72 of 100
(7607 views)
Shortcut
Registered: May 15, 2004
Posts: 432
|
And, if you have to give 30% initial slack to just start seeing benefits, then a dynamic belay has to be better!
|
|
|
 |
 |

jt512
Sep 4, 2010, 2:38 AM
Post #73 of 100
(7598 views)
Shortcut
Registered: Apr 12, 2001
Posts: 21904
|
112 wrote: And, if you have to give 30% initial slack to just start seeing benefits, then a dynamic belay has to be better!
Again, a dynamic belay does not negate leaving slack. And 30% slack is no big deal. If the leader were laterally out, say, six from his pro, it would be no big deal to have as much as six feet of slack in the rope: 100%.
Jay
|
|
|
 |
 |

jt512
Sep 4, 2010, 2:44 AM
Post #74 of 100
(7590 views)
Shortcut
Registered: Apr 12, 2001
Posts: 21904
|
Question for the physics people: Does fall factor matter?
Jay
|
|
|
 |
 |

curt
Sep 4, 2010, 3:51 AM
Post #75 of 100
(7579 views)
Shortcut
Registered: Aug 27, 2002
Posts: 18275
|
jt512 wrote: Question for the physics people: Does fall factor matter? Jay
It should. If the belayer is not anchored at the base of the roof (as in ptlong2's diagram above) and is instead belaying from 100ft farther below (for example) there is already a mechanism in the system that mimics paying out slack--i.e., greater rope stretch.
Curt
|
|
|
 |
|

|